Model selection for high dimensional data with applications toward genetics
To apply:Official announcement
Deadline : 30.Apr.2021
PhD Position
We invite applications for a fully funded PhD position with a project on model selection for high dimensional data with applications in genetics at Lund University. The two main coordinators of the project are Małgorzata Bogdan and Jonas Wallin.
We are looking for a student who fits into one of the following two directions in statistics:
biostatics track
Here the students has a
- MSc in mathematics, statistics, computer science, biostatistics or physics
- Sound knowledge of applied statistics (linear models, Bayesian statistics)
- Strong programing skills (R and/or C++ )
- Ability to work in an interdisciplinary team at the interface of genetics, computer science and statistics.
mathematical track
Here the students has a
- MSc in mathematics of statistics
- Strong mathematical skills (probability, functional analysis, linear algebra)
- Some experince in programming
Project Description
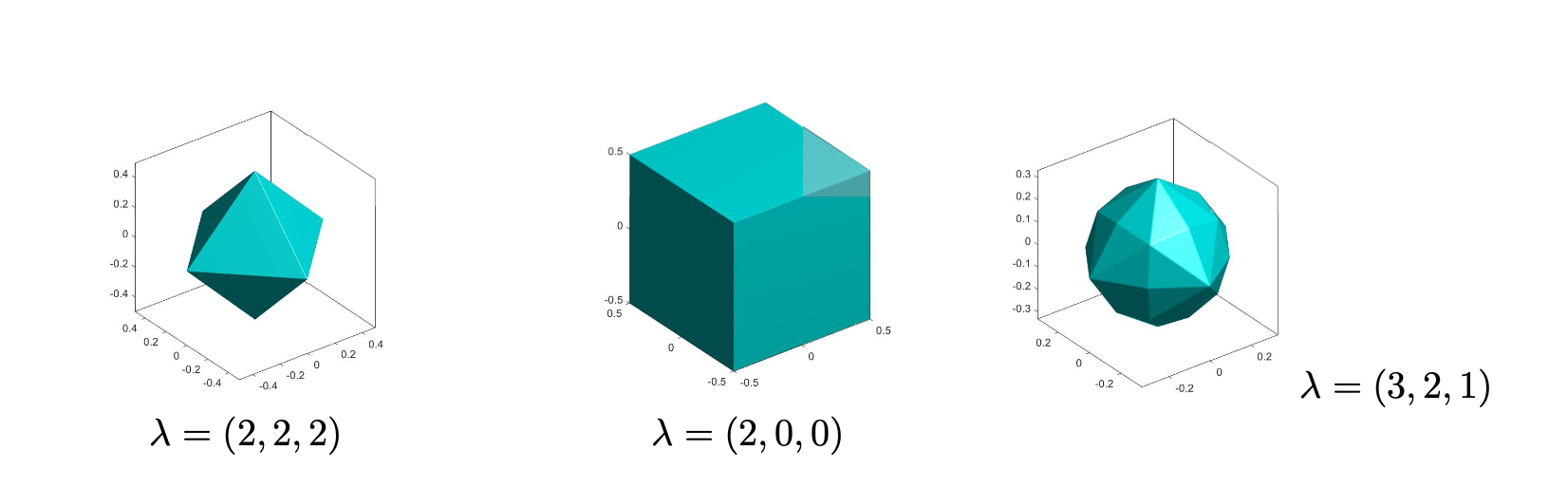
In previous projects (see [1], [2]), we developed SLOPE, the convex model selection and estimation procedure for high-dimensional statistical problems. Different versions of the “SLOPE ball” can be seen in the figure at the top of the page. Recently, we have also developed an Adaptive Bayes version of SLOPE (ABSLOPE) [3] that allows the incorporation of prior knowledge and can handle latent variables such as missing data. Despite several important articles pointing out desirable properties of SLOPE (see [4], [5], [6]), the mathematical theory of SLOPE is not yet fully developed. The PhD student who chooses the mathematical-statistical route of the project will be involved in the development of new mathematical results concerning the asymptotic properties of SLOPE and ABSLOPE, including the asymptotic control of the false discovery rate or the study of the prediction accuracy.
The applied part of the project will mainly deal with gene identification. In our recent article [7], we showed that over-simplified statistical models can lead to many false gene discoveries. We also showed that this problem can be solved by adding a random effect describing the polygenic background. The difference between the two methods is shown at the bottom of the page, with the top of the figures illustrating the results of the classical method and the bottom of the figures illustrating our new method. In the present project, we plan to extend this approach to deal with the variability of polygenic background along the chromosome. The estimation problem will be addressed by developing a suitable version of ABSLOPE. This will also require speeding up the ABSLOPE algorithm. The PhD student who chooses the applied route will be involved in research to accelerate the algorithm (see e.g. [8]) and/or in the development of a methodology for gene identification.
References
- M. Bogdan, E. van den Berg, C. Sabatti, W. Su, and E. J. Candes. SLOPE – adaptive variable selection via convex optimization. Annals of Applied Statistics, 9(3):1103–1140, 2015.
- D. Brzyski, A. Gossmann, W. Su, and M. Bogdan. Group SLOPE - adaptive selection of groups of predictors. Journal of the American Statistical Association, 114:419–433, 2019.
- W. Jiang, M. Bogdan, J. Josse, B. Miasojedow, V. Rockova, TB Group. Adaptive Bayesian SLOPE–High-dimensional Model Selection with Missing Values, arXiv:1909.06631, 2019.
- W. Su and E.J. Candes. SLOPE is adaptive to unknown sparsity and asymptotically minimax. Annals of Statistics, 40:1038–1068, 2016.
- P.C. Bellec, G. Lecu´e, and A.B. Tsybakov. Slope meets lasso: Improved oracle bounds and optimality. Annals of Statistics, 46(6B):3603–3642, 2018.
- F. Abramovich and V. Grinshtein. High-dimensional classification by sparse logistic regression. IEEE Transactions on Information Theory, 65:3068–3079, 2019.
- J. Wallin, M. Bogdan, P. A. Szulc, R.W. Doerge, and D.O. Siegmund. Ghost QTL and Hotspots in experimental crosses— novel approach for modeling polygenic effects. Genetics, 2021. doi:10.1093/genetics/iyaa041.
- J. Larsson, M. Bogdan, and J. Wallin. The strong screening rule for SLOPE. Advances in Neural Information Processing Systems 33 (NeurIPS 2020), 2020.

